Number Of Electrons In Helium
- Number Of Electrons In Helium
- Number Of Electrons In Helium 3
- Element With 4 Electrons
- Number Of Electrons Gained Or Lost In Helium
Quantum Numbers: H to Ne
There are four quantum numbers: n, ℓ, mℓ, and ms. Each one is a particular factor in an equation describing a property of the electron. At this introductory level, the equations are not needed. The value of each quantum number is assigned to each electron in an atom by a 'building up' process. Niels Bohr called this process the 'Aufbau' principle: aufbau means 'building up.'
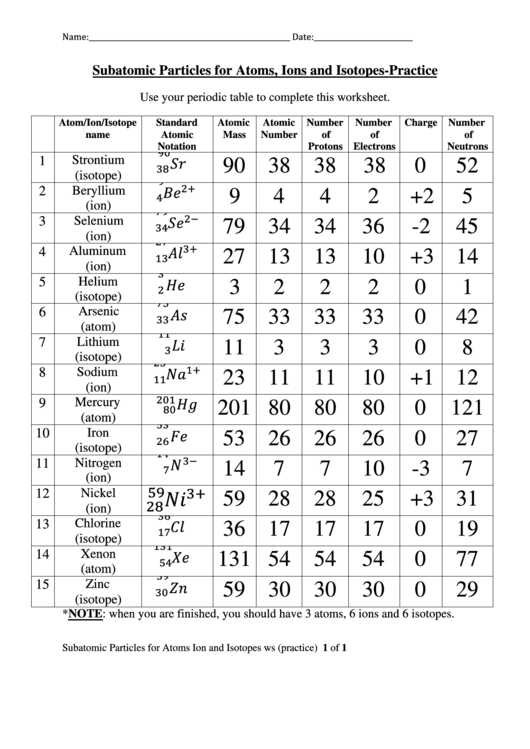
How Many Valence Electrons Does Helium Have? Number of Valence Electrons in Helium Why does helium only have two valence electrons?Read My Blogpost:https:/. The helium ground state consists of two identical 1s electrons. The energy required to remove one of them is the highest ionization energy of any atom in the periodic table: 24.6 electron volts. The energy required to remove the second electron is 54.4 eV, as would be expected by modeling it after the hydrogen energy levels.
- Answer: helium 2.
- Atomic Number of Helium Helium is a chemical element with atomic number 2 which means there are 2 protons and 2 electrons in the atomic structure. The chemical symbol for Helium is.
n is ALWAYS the starting point for building up a series of quantum numbers. Each quantum number is then assigned according to a set of rules, each of which took years of study to finally determine. The rules ARE NOT just any old arbitrary ones; they have been determined from a study of nature. Remember the rules:
(1) n = 1, 2, 3, and so on.
(2) ℓ = 0, 1, 2, . . . , n - 1
(3) mℓ starts at negative ℓ, runs by whole numbers to zero and then goes to positive ℓ.
(4) after the n, ℓ and mℓ to be used have been determined, assign the ms value +½ to one electron, then assign the ms value of -½ to the next electron, while using the same n, ℓ and m values.
Also, keep in mind that we use only one n, ℓ, mℓ, and ms value each to make a set of four quantum numbers for each electron. It is this set of four quantum numbers that uniquely identifies each electron.
Last point: the last column in each table below is called 'Orbital Name.' As you are reading this tutorial, you may not yet know what an orbital is. That's OK, but please understand the concept called 'orbital' is an important one. Here's a real simple description that ignores lots of details: each orbital is a region of space around the nucleus which contains a MAXIMUM of two electrons. Realize that it's more complex than that, but the above description is good enough for now. I hope!!
Hydrogen - one electron
First Electron
n = 1
ℓ = 0
mℓ = 0
In each case, note that we start with the smallest value of n, ℓ, or mℓ possible. Make sure you look over the rules to see how each value was arrived at. ℓ starts at zero and goes to n - 1, which is zero since we get 1 - 1 = 0, when using n = 1. When ℓ = 0, there is only one possible choice for mℓ, which must be zero.
ms = +½
This completes the four quantum numbers for the single electron possessed by hydrogen. I shall build up a table like this:
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 1 | Hydrogen | 1 | 0 | 0 | +½ | 1s |
Helium - two electrons
First Electron
n = 1
ℓ = 0
mℓ = 0
ms = +½
The first electron in helium has exactly the same four quantum number of the first electron in hydrogen. However, helium has TWO electrons. So we 'build up' from the previous electrons by adding one more.
Second Electron
n = 1
ℓ = 0
mℓ = 0
ms = -½
Notice the same n, ℓ, and mℓ values, but ms has shifted from positive ½ to negative ½. This was the problem Pauli saw in 1925. Three quantum numbers was insufficient to UNIQUELY identify each electron, but a fourth one (the one called ms) did the trick.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 2 | Helium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ |
Lithium - three electrons
The first two electrons quantum numbers' are EXACTLY the same as the two in helium:
1, 0, 0, +½ and 1, 0, 0, -½
Third Electron: here's where we 'build up' by adding one more electron. Zip cleaner mac.
However, we are now presented with a problem. All the values with n = 1 have been used up, but we have only accounted for two of lithium's three electrons. What to do about the third?
Answer: start with the NEXT n value; n = 2. However, there is a problem with ℓ; do we use ℓ = 0 or ℓ = 1, since both are possible with n = 2?
Answer: start with the lowest value first, so that means using ℓ = 0. (Don't worry, we will use ℓ = 1 soon enough.)
Figuring out mℓ should be easy; when ℓ = 0, mℓ can only equal 0. So n, ℓ, mℓ for the third electron is 2, 0, 0. I'll add in ms in the table below.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 3 | Lithium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s |
Beryllium - four electrons
In the building up process, we go one electron at a time. Therefore, we will use the three from lithium and add one more.
Fourth Electron
n = 2
ℓ = 0
mℓ = 0
ms = -½ Hackintosh mavericks.
Notice the same n, ℓ, and m values as the third electron, but ms for the fourth electron has shifted from positive ½ to negative ½.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 4 | Beryllium | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ |
Pretty easy, eh? It stays easy, if you follow the rules. With beryllium, we have exhausted the possibilities for the n = 2; ℓ = 0 combination. However, when n = 2, ℓ can take on another value, namely ℓ = 1. This has consequences for the mℓ value as well and, after we finish, there will be six electrons that have a combination of n = 2 and ℓ = 1.
Here's the rule for mℓ again: start at negative ℓ, run by whole numbers to zero and then go to positive ℓ. Since ℓ = 1, we start with -1, go to zero and end up at +1. This gives us three values for mℓ when ℓ = 1. Hopefully you can see that, since ms takes on +½ and -½, we will wind up with six sets of quantum numbers.
Warning: there's going to be a new rule introduced after boron. So prepare yourself because, just as you thought it was getting easy, there gets added some new stuff. By the way, us mean old teachers didn't make all this stuff up to torture poor chemistry students. Nature really does do what I will explain below. Here's boron:
Boron - five electrons

Following the usual pattern, I've repeated the previous four electrons. As we go on to the ℓ = 1 values, keep in mind that we will start with the lowest value of mℓ, namely negative one.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 5 | Boron | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px |
Eventually, I will wind up with three orbital names. 2px is just the first, x meaning the x-axis. Next will be 2py, for the y-axis and the last name used will be 2pz, for the z-axis. These three orbitals are oriented at 90° to each other.
Hund's Rule (named for Fredrich Hund) is the name of the new rule. This rule concerns the relationship between the ℓ and mℓ quantum numbers. When ℓ = 0, mℓ can only equal zero and Hund's Rule does not show up. However, now that we have reached ℓ = 1, mℓ can take on multiple values. Hund's Rule concerns the order in which we assign the ℓ and mℓ values.
By the way, I'm going to avoid a technical statement of Hund's Rule for the moment. I'll discuss how it works first.
Hund's Rule means that we will use each possible ℓ, mℓ combination ONCE before going back and using it a second time. Here are the three possible ℓ, mℓ combos when ℓ = 1:
| ℓ | mℓ |
| 1 | -1 |
| 1 | 0 |
| 1 | +1 |
For boron, we have used the ℓ, mℓ combination of 1, -1. The key is to see that Hund's Rule requires we go on to the NEXT ℓ, mℓ combination for the next element: carbon.
Carbon - six electrons
Following the usual pattern, I've repeated the previous five electrons. As we continue on with the ℓ = 1 values, keep in mind that Hund's Rule will affect how we assign the next mℓ value.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 6 | Carbon | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | 0 | +½ | 2py |
Nitrogen - seven electrons
Macos extract 7z. Since we still have not first used all possible ℓ, mℓ values ONCE, we go on to the next ℓ, mℓ combination.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 7 | Nitrogen | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | +1 | +½ | 2pz |
2px, 2py and 2pz are three different orbitals, each one capable of holding two electrons. Notice how, in nitrogen, each of the three orbitals is filled up HALF-WAY (that is, with one electron) before we go back and fill up each orbital with the second electron.
This 'half-filled orbital' has definite chemical consequences. Remember it well. Also, using 2px first, then going to y and then z is purely convention. The x, y, z order is not of consequence in the above examples. However keep in mind the using each letter ONCE first being using it for the second electron is important.
Oxygen - eight electrons
Now that we have used each ℓ, mℓ combination once, we proceed to go back and use each combo the second time. For oxygen to neon, I've marked which electron is the one added.
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 8 | Oxygen | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| this one added | ---> | 2 | 1 | -1 | -½ | |
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | +1 | +½ | 2pz |
Fluorine - nine electrons
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 9 | Fluorine | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | -1 | -½ | |||
| 2 | 1 | 0 | +½ | 2py | ||
| this one added | ---> | 2 | 1 | 0 | -½ | |
| 2 | 1 | +1 | +½ | 2pz |
Neon - ten electrons
| Atomic Number | Element | n | ℓ | mℓ | ms | Orbital Name |
| 10 | Neon | 1 | 0 | 0 | +½ | 1s |
| 1 | 0 | 0 | -½ | |||
| 2 | 0 | 0 | +½ | 2s | ||
| 2 | 0 | 0 | -½ | |||
| 2 | 1 | -1 | +½ | 2px | ||
| 2 | 1 | -1 | -½ | |||
| 2 | 1 | 0 | +½ | 2py | ||
| 2 | 1 | 0 | -½ | |||
| 2 | 1 | +1 | +½ | 2pz | ||
| this one added | ---> | 2 | 1 | +1 | -½ |

We have now completed all possible values for n = 1 AND n = 2. Starting with element 11, sodium, we will proceed on to n = 3. When we finish, we will have used ℓ = 0, ℓ = 1 (and applied Hund's Rule again) and then, before going on to ℓ = 3, we will hit another interesting twist that nature has handed us. We will wind up going on to n = 4 and then coming back to finish n = 3. It will be fun!
Learning Outcomes
- Describe the behavior and location of electrons, and how these factors influence bond formation between atoms
Electron Shells and the Bohr Model
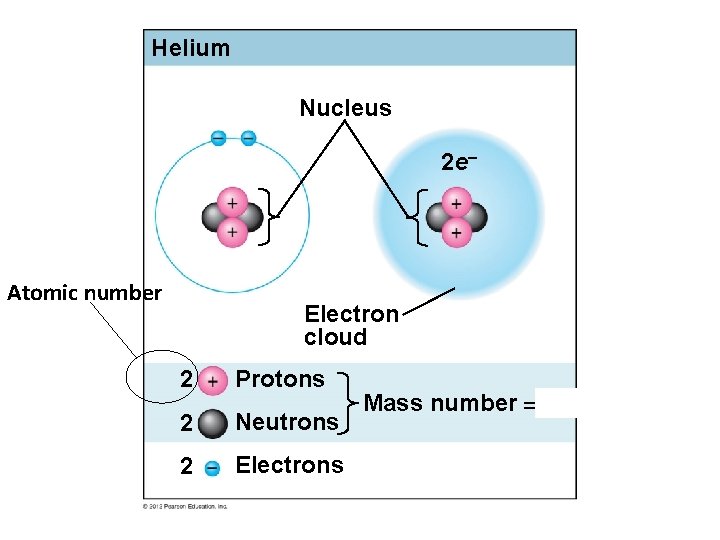
It should be stressed that there is a connection between the number of protons in an element, the atomic number that distinguishes one element from another, and the number of electrons it has. In all electrically neutral atoms, the number of electrons is the same as the number of protons. Thus, each element, at least when electrically neutral, has a characteristic number of electrons equal to its atomic number.
An early model of the atom was developed in 1913 by Danish scientist Niels Bohr (1885–1962). In this model, electrons exist within principal shells. An electron normally exists in the lowest energy shell available, which is the one closest to the nucleus. Energy from a photon of light can bump it up to a higher energy shell, but this situation is unstable, and the electron quickly decays back to the ground state. In the process, a photon of light is released.
The Bohr model shows the atom as a central nucleus containing protons and neutrons, with the electrons in circular orbitals at specific distances from the nucleus, as illustrated in Figure 1. These orbits form electron shells or energy levels, which are a way of visualizing the number of electrons in the outermost shells. These energy levels are designated by a number and the symbol “n.” For example, 1n represents the first energy level located closest to the nucleus.
Electrons fill orbitals in a consistent order: they first fill the orbitals closest to the nucleus, then they continue to fill orbitals of increasing energy further from the nucleus. If there are multiple orbitals of equal energy, they will be filled with one electron in each energy level before a second electron is added. The electrons of the outermost energy level determine the energetic stability of the atom and its tendency to form chemical bonds with other atoms to form molecules.
Under standard conditions, atoms fill the inner shells first, often resulting in a variable number of electrons in the outermost shell. The innermost shell has a maximum of two electrons but the next two electron shells can each have a maximum of eight electrons. This is known as the octet rule, which states, with the exception of the innermost shell, that atoms are more stable energetically when they have eight electrons in their valence shell, the outermost electron shell. Examples of some neutral atoms and their electron configurations are shown in Figure 2. Notice that in this figure, helium has a complete outer electron shell, with two electrons filling its first and only shell. Similarly, neon has a complete outer 2n shell containing eight electrons. In contrast, chlorine and sodium have seven and one in their outer shells, respectively, but theoretically they would be more energetically stable if they followed the octet rule and had eight.
Practice Question
Figure 2. Bohr diagrams for hydrogen, helium, lithium, carbon, fluorine, neon, sodium, silicon, chlorine, and argon.
Bohr diagrams indicate how many electrons fill each principal shell. Group 18 elements (helium, neon, and argon are shown in Figure 2) have a full outer, or valence, shell. A full valence shell is the most stable electron configuration. Elements in other groups have partially filled valence shells and gain or lose electrons to achieve a stable electron configuration.
An atom may give, take, or share electrons with another atom to achieve a full valence shell, the most stable electron configuration. Looking at this figure, how many electrons do elements in group 1 need to lose in order to achieve a stable electron configuration? How many electrons do elements in groups 14 and 17 need to gain to achieve a stable configuration?
Show AnswerUnderstanding that the organization of the periodic table is based on the total number of protons (and electrons) helps us know how electrons are distributed among the outer shell. The periodic table is arranged in columns and rows based on the number of electrons and where these electrons are located. Take a closer look at the some of the elements in the periodic table’s far right column in Figure 3.
Figure 3. The periodic table shows the atomic mass and atomic number of each element. The atomic number appears above the symbol for the element and the approximate atomic mass appears below it.
The group 18 atoms helium (He), neon (Ne), and argon (Ar) all have filled outer electron shells, making it unnecessary for them to share electrons with other atoms to attain stability; they are highly stable as single atoms. Their non-reactivity has resulted in their being named the inert gases (or noble gases). Compare this to the group 1 elements in the left-hand column. These elements, including hydrogen (H), lithium (Li), and sodium (Na), all have one electron in their outermost shells. That means that they can achieve a stable configuration and a filled outer shell by donating or sharing one electron with another atom or a molecule such as water. Hydrogen will donate or share its electron to achieve this configuration, while lithium and sodium will donate their electron to become stable. As a result of losing a negatively charged electron, they become positively charged ions. Group 17 elements, including fluorine and chlorine, have seven electrons in their outmost shells, so they tend to fill this shell with an electron from other atoms or molecules, making them negatively charged ions. Group 14 elements, of which carbon is the most important to living systems, have four electrons in their outer shell allowing them to make several covalent bonds (discussed below) with other atoms. Thus, the columns of the periodic table represent the potential shared state of these elements’ outer electron shells that is responsible for their similar chemical characteristics.
Electron Orbitals
Although useful to explain the reactivity and chemical bonding of certain elements, the Bohr model of the atom does not accurately reflect how electrons are spatially distributed surrounding the nucleus. They do not circle the nucleus like the earth orbits the sun, but are found in electron orbitals. These relatively complex shapes result from the fact that electrons behave not just like particles, but also like waves. Mathematical equations from quantum mechanics known as wave functions can predict within a certain level of probability where an electron might be at any given time. The area where an electron is most likely to be found is called its orbital.
Number Of Electrons In Helium
Figure 4. Click for a larger image. The s subshells are shaped like spheres. Both the 1n and 2n principal shells have an s orbital, but the size of the sphere is larger in the 2n orbital. Each sphere is a single orbital. p subshells are made up of three dumbbell-shaped orbitals. Principal shell 2n has a p subshell, but shell 1 does not.
Recall that the Bohr model depicts an atom’s electron shell configuration. Within each electron shell are subshells, and each subshell has a specified number of orbitals containing electrons. While it is impossible to calculate exactly where an electron is located, scientists know that it is most probably located within its orbital path. Subshells are designated by the letters s, p, d, and f. The s subshell is spherical in shape and has one orbital. Principal shell 1n has only a single s orbital, which can hold two electrons. Principal shell 2n has one s and one p subshell, and can hold a total of eight electrons. The p subshell has three dumbbell-shaped orbitals, as illustrated in Figure 4. Subshells d and f have more complex shapes and contain five and seven orbitals, respectively. These are not shown in the illustration. Principal shell 3n has s, p, and d subshells and can hold 18 electrons. Principal shell 4n has s, p, d and f orbitals and can hold 32 electrons. Moving away from the nucleus, the number of electrons and orbitals found in the energy levels increases. Progressing from one atom to the next in the periodic table, the electron structure can be worked out by fitting an extra electron into the next available orbital.
The closest orbital to the nucleus, called the 1s orbital, can hold up to two electrons. This orbital is equivalent to the innermost electron shell of the Bohr model of the atom. It is called the 1s orbital because it is spherical around the nucleus. The 1s orbital is the closest orbital to the nucleus, and it is always filled first, before any other orbital can be filled. Hydrogen has one electron; therefore, it has only one spot within the 1s orbital occupied. This is designated as 1s1, where the superscripted 1 refers to the one electron within the 1s orbital. Helium has two electrons; therefore, it can completely fill the 1s orbital with its two electrons. This is designated as 1s2, referring to the two electrons of helium in the 1s orbital. On the periodic table Figure 4, hydrogen and helium are the only two elements in the first row (period); this is because they only have electrons in their first shell, the 1s orbital. Hydrogen and helium are the only two elements that have the 1s and no other electron orbitals in the electrically neutral state.
The second electron shell may contain eight electrons. This shell contains another spherical s orbital and three “dumbbell” shaped p orbitals, each of which can hold two electrons, as shown in Figure 4. After the 1s orbital is filled, the second electron shell is filled, first filling its 2s orbital and then its three p orbitals. When filling the p orbitals, each takes a single electron; once each p orbital has an electron, a second may be added. Lithium (Li) contains three electrons that occupy the first and second shells. Two electrons fill the 1s orbital, and the third electron then fills the 2s orbital. Its electron configuration is 1s22s1. Neon (Ne), on the other hand, has a total of ten electrons: two are in its innermost 1s orbital and eight fill its second shell (two each in the 2s and three p orbitals); thus, it is an inert gas and energetically stable as a single atom that will rarely form a chemical bond with other atoms. Larger elements have additional orbitals, making up the third electron shell. While the concepts of electron shells and orbitals are closely related, orbitals provide a more accurate depiction of the electron configuration of an atom because the orbital model specifies the different shapes and special orientations of all the places that electrons may occupy.
Watch this visual animation to see the spatial arrangement of the p and s orbitals. Note that this video has no audio.
Number Of Electrons In Helium 3
Element With 4 Electrons
You can view the audio description text for “Atomic Orbitals – Electron Configuration of Scandium” here (opens in new window).
Video Review
This video gives another overview of the electron:
Contribute!
Number Of Electrons Gained Or Lost In Helium
